lunes, 10 de febrero de 2014

Función trigonométrica

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos.

Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo: $\alpha$ , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo $\alpha$ .
El cateto adyacente (b) es el lado adyacente al ángulo $\alpha$ .

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a π radianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sin \alpha ={\frac {{\color {ForestGreen}{\textrm {opuesto}}}}{{\color {Red}{\textrm {hipotenusa}}}}}={\frac {a}{h}}.$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo $\alpha$ , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha ={\frac {{\color {Blue}{\textrm {adyacente}}}}{{\color {Red}{\textrm {hipotenusa}}}}}={\frac {b}{h}}.$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha ={\frac {{\color {ForestGreen}{\textrm {opuesto}}}}{{\color {Blue}{\textrm {adyacente}}}}}={\frac {a}{b}}.$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha ={\frac {{\color {Blue}{\textrm {adyacente}}}}{{\color {ForestGreen}{\textrm {opuesto}}}}}={\frac {b}{a}}.$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha ={\frac {{\color {Red}{\textrm {hipotenusa}}}}{{\color {Blue}{\textrm {adyacente}}}}}={\frac {h}{b}}.$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha ={\frac {{\color {Red}{\textrm {hipotenusa}}}}{{\color {ForestGreen}{\textrm {opuesto}}}}}={\frac {h}{a}}.$

Funciones trigonométricas de ángulos notables

	0°	30°	45°	60°	90°
sen	0	${\frac {1}{2}}$	${\frac {{\sqrt {2}}}{2}}$	${\frac {{\sqrt {3}}}{2}}$	1
cos	1	${\frac {{\sqrt {3}}}{2}}$	${\frac {{\sqrt {2}}}{2}}$	${\frac {1}{2}}$	0
tan	0	${\frac {{\sqrt {3}}}{3}}$	1	${\sqrt {3}}$	$\infty$

domingo, 2 de febrero de 2014

Triángulos

Definición de triángulo: Un triángulo es un polígono de tres lados.

Propiedades de los triángulos:

1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
2 La suma de los ángulos interiores de un triángulo es igual a 180°.
3 El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.

Clasificacion por sus ángulos

Los ángulos complementarios son aquellos ángulos cuyas medidas suman 90º (grados sexagesimales). Si dos ángulos complementarios son consecutivos, los lados no comunes de los dos forman un ángulo recto.

Los ángulos suplementarios son aquellos cuya suma de medidas es 180° (grados sexagesimales).
Así, para obtener el ángulo suplementario β de un determinado ángulo α comprendido entre [0,180º], se restará α a 180°, de manera que:

β = 180° – α

En otras unidades de medida del ángulo plano, 180 grados sexagesimales equivalen a π radianes, o 200 grados centesimales y 360 grados sexagesimales equivalen a 2π radianes, o 400 grados centesimales.

Clasificación de los triángulos:

Según sus lados:

Triángulo equilátero

Tres lados iguales

Triángulo isósceles

Dos lados iguales

Triángulo escaleno

Tres lados desiguales

Según sus ángulos

Triángulo acutángulo

Tres ángulos agudos

Triángulo rectángulo

Un ángulo recto.
El lado mayor es la hipotenusa.
Los lados menores son los catetos.

Triángulo obtusángulo

Un ángulo obtuso.

Alturas, medianas, mediatrices y bisectrices de un triángulo

Alturas de un triángulo

Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).

Ortocentro

Es el punto de corte de las tres alturas.

Medianas de un triángulo

Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.

Baricentro

Es el punto de corte de las tres medianas.
El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.

BG = 2GA

Mediatrices de un triángulo

Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.

Circuncentro

Es el punto de corte de las tres mediatrices.
Es el centro de una circunferencia circunscrita al triángulo.

Bisectrices de un triángulo

Bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.

Incentro

Es el punto de corte de las tres bisetrices.
Es el centro de una circunferencia inscrita en el triángulo.

EJERCICIOS DE LA RECTA EN EL PLANO

Si el punto medio M tiene coordenadas. M (x _m, y _m) entonces:

Luego, las coordenadas del punto M son. M (1, 1/2)

b) Como

entonces

Si P(x, y) denota las coordenadas del punto P, se tiene de acuerdo a las fórmulas (5) y (6):

Luego, las coordenadas del punto P, son: P

RECTAS EN EL PLANO CARTESIANO

La recta o la línea recta, se extiende en una misma dirección, existe en una sola dimensión y contiene infinitos puntos ; está compuesta de infinitos segmentos (el fragmento de linea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, es decir, no posee principio ni fin.

Ecuación de la recta

Pendiente y ordenada al origen

En una recta, la pendiente $m\,$ es siempre constante. Se calcula mediante la ecuación:

$m = \left( \frac{y_2 - y_1}{x_2 - x_1} \right)$
Se puede obtener la ecuación de la recta a partir de la fórmula de la pendiente (ecuación punto-pendiente):

$y - y_1 = m (x - x_1)\!$

Esta forma de obtener la ecuación de una recta se suele utilizar cuando se conocen su pendiente y las coordenadas de uno de sus puntos, o cuando se conocen sólo los dos puntos, por lo que también se le llama ecuación de la recta conocidos dos puntos. La pendiente $m$ es la tangente del ángulo que forma la recta con el eje de abscisa X.
La ecuación de la recta que pasa por el punto $P_1 = (x_1, y_1) \,$ y tiene la pendiente dada $m$ es:

$y - y_1 = m (x - x_1)\,$

Ejemplo

La ecuación de la recta que pasa por el punto A $(2, -4)$ y que tiene una pendiente de $-\frac{1}{3}$ .
Al sustituir los datos en la ecuación, resulta lo siguiente:

$y - y_1 = m (x - x_1)\!$ $y - ( - 4) = - 1/3 (x - 2)\!$ $3 (y + 4) = - 1(x - 2)\!$ $3y + 12 = - x + 2\!$ $x + 3y + 12 = 2\!$

$x + 3y + 10 = 0\!$

Forma simplificada de la ecuación de la recta

Si se conoce la pendiente m, y el punto donde la recta corta al eje de ordenadas es (0, b), podemos deducir, partiendo de la ecuación general de la recta, $y - y_1 = m (x - x_1)$ :

$y - b = m (x - 0)\!$ $y - b = m x \!$

$y = m x + b \!$

Esta es la segunda forma de la ecuación de la recta y se utiliza cuando se conoce la pendiente y la ordenada al origen, que llamaremos $b$ . También se puede utilizar esta ecuación para conocer la pendiente y la ordenada al origen a partir de una ecuación dada.

Forma segmentaria de la ecuación de la recta (Ecuación simétrica)

Así como a la ordenada al origen se le puede llamar $b$ , a la abscisa al origen se le puede llamar $a$ . Si se plantea como problema encontrar la ecuación de una recta, conocidos $a$ y $b$ (la abscisa y ordenada al origen), se conocen dos puntos de la recta los cuales son los siguientes:

$(0, b)\!$ y $(a, 0)\!$

Con estos puntos se puede encontrar dicha ecuación, pero primero se debe calcular la pendiente:

$m = \left( \frac{0 - b}{a - 0} \right) = \frac{-b}{a}$

Después se sustituye en la ecuación $y - y_1 = m (x - x_1)$ , usando cualquiera de los dos puntos, en este caso (a, 0):

$ay = - bx + ab\!$

$bx + ay = ab\!$

Por último se tiene que dividir toda la ecuación entre el término independiente $ab$ :

$\frac{bx}{ab} + \frac{ay}{ab} = \frac{ab}{ab}\!$

$\frac{x}{a} + \frac{y}{b} = 1 \!$

Se obtiene la ecuación de la recta en su forma simétrica. Esta ecuación se suele utilizar para obtener la ecuación de una recta de la que se conocen sus intersecciones con los ejes y cuando, a partir de la ecuación de una recta, se desean conocer los puntos donde dicha recta interseca a los ejes.

Ecuación normal de la recta

Esta es la forma normal de la recta:

$x \ cos\omega + y \ sen\omega - d = 0 \!$

Siendo d el valor de la distancia entre la recta y el origen de coordenadas. El ángulo omega ω es el ángulo formado entre la recta y el eje de las ordenadas.
Donde x que es una constante que nos ayudará a obtener la forma normal, la cual se puede obtener de la forma general de la recta.

$Ax + By + C = 0 \!$

Extrayendo la raiz cuadrada de la suma de los cuadrados de B X A. Como sigue:

$x = \sqrt{A^2 + B^2}$

Con el número x podemos obtener a $cos\omega$ y a $sen\omega$ de la misma ecuación general de la recta, dividiendo a A y B entre k y para calcular d dividimos a C entre k.

Debemos tener cuidado al calcular C, por que C=-kd, entonces si C>0 (es positiva) tomaremos el valor negativo de k (y será el mismo todas las veces que usemos a k en la misma ecuación), cuando C<0 (es negativa) usaremos el valor positivo de k.³

Ecuación normal de la recta (Segunda forma)

$\frac{Ax+By+C}{\sqrt{A^2 + B^2}}=0$

Tomando el valor positivo o negativo de la raíz según corresponda.

Rectas notables

Rectas perpendiculares.

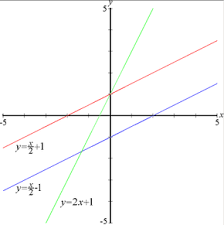
La ecuación de una recta vertical responde a la ecuación general $x = x_v$ (constante).

La ecuación de una recta horizontal responde a la ecuación general $y = y_h$ (constante).

Una recta trigonoidal que pase por el origen O (0, 0), cumplirá la condición b = 0, siendo su ecuación: $y = (m)(x)\;$ .
recta secante
recta tangente

Dos rectas cualesquiera:

$y = \left( m_1 \right)\left( x \right)+ b_1 \!$

$y = \left( m_2 \right)\left( x \right)+ b_2 \!$

serán paralelas si y solo si $m_1 = m_2\;$ . Además, serán coincidentes cuando: $b_1 = b_2\;$

serán perpendiculares si y sólo si $m_1 = -1/ m_2\;$ , es decir: $(m_1)(m_2) = -1 \;$

Rectas que pasan por un punto

Rectas que pasan por el punto: (2,4)

Determinar las rectas del plano que pasan por el punto $(x_0, y_0) \,$ .
La ecuación de la recta ha de ser, como ya se sabe:

$y = m x + b \,$

Y ha de pasar por el punto $(x_0, y_0) \,$ , luego tendrá que cumplirse:

$y_0 = m x_0 + b \,$

Despejando b, tenemos esta ecuación:

$b= y_0 - m x_0 \,$

Sustituyendo b en la ecuación general de la recta:

$y = m x + (y_0 - m x_0) \,$

Ordenando términos:

$y = m (x- x_0) + y_0 \,$

Esta ecuación define un haz de rectas en el plano que pasa por el punto $(x_0, y_0)$ , el valor de m es la pendiente de cada una de las rectas que forman parte del haz, m puede tomar un valor real cualesquiera.

Recta que pasa por dos puntos

Si ha de pasar por dos puntos $(x_1, y_1)$ y $(x_2, y_2)$ luego tendrá que cumplirse:

$y_{1} = m x_{1} + b \,$

$y_{2} = m x_{2} + b \,$

Ambas forman un sistema de dos ecuaciones con dos incógnitas m y b, para resolver este sistema, eliminamos una de las incognitas b restando m.a.m la segunda ecuación de la primera para obtener:

$y_1 - y_2 = m x_1 - m x_2 \,$

agrupando términos:

$y_1 - y_2 = m (x_1 - x_2) \,$

despejando m:

$m= \cfrac{y_1 - y_2}{x_1 - x_2} \,$

este valor, m, es el de la pendiente de la recta que pasa por los dos puntos: $(x_1, y_1)$ y $(x_2, y_2)$ . Despejando ahora el valor de b de una de las ecuaciones del sistema, por ejemplo de la primera, tenemos:

$b = y_1 - m x_1 \,$

y sustituyendo m, por su valor ya calculado;

$b = y_1 - \cfrac{y_1 - y_2}{x_1 - x_2} \; x_1 \,$

Tenemos las dos incógnitas m y b despejadas, en función de las coordenadas de los dos puntos por los que tienen que pasar, entonces la ecuación general de la recta, con los parámetros ya calculados es:

$y = \cfrac{y_1 - y_2}{x_1 - x_2} \; x + y_1 - \cfrac{y_1 - y_2}{x_1 - x_2} \; x_1$

Que también puede expresarse:

$y = \cfrac{y_1 - y_2}{x_1 - x_2} \; (x - x_1) + y_1$

Ecuación general de la recta

Es la expresión Ax + By + C = 0 , donde A y B no pueden valer cero simultáneamente.
-A/B representa la pendiente y -C/B señala la ordenada en el origen. Datos suficientes para representar la ecuación en el plano cartesiano XOY.

MODULO 3 (MATEMATICAS)

CONTADOR DE VISITAS